これは 帰ってきた AOJ-ICPC Advent Calendar 2022 の16日目です。
問題概要
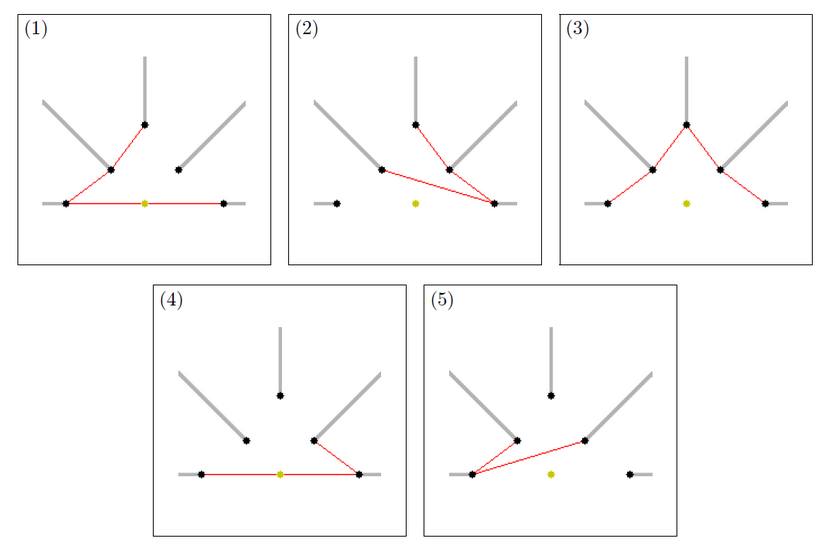
xy平面上に $N$ 個のポールが存在し、その座標が与えられる。また、原点に光源が存在し、それぞれのポールが存在する方向に影を形成する。ただし、影の長さは無限に続くものとする。
Alice と Bob は次の遊びを行うとする。
始点終点となるポールのペアを1つ選択する(始点と終点の一致も許容)。
影を通過せずに、ポール $i$ からポール $j$ に移動する最短距離を
とする。始点のポールを $s$、終点のポールを $g$ とした時に、
が最大となるような $i$ を選択する。
この遊びによる移動距離は、
である。
この時、次の $P$ 個のクエリを処理せよ。
各クエリでは整数
が与えられる。
始点を
、終点を
の範囲からランダムに選択する。
その始点終点による上記の遊びの移動距離の期待値を出力。
制約
同一の座標に2個以上のポールが存在しない。また、あるポールの影に被る座標や、原点にポールが存在することもない。
解法
この問題は、大きく3つのステップに分けて解くことができます。
全ての頂点対
について、最短距離
を
で求める。
全ての頂点対
について、それぞれを始点終点とした場合の遊びの移動距離を
で求める。
各クエリに
で答えられるように前計算を行う。
1番目は比較的容易です。2番目が本質で、これを求めることが可能!と分かった状態で問題を考えると、クエリがおまけになっていることが分かります。というのも、2番目の結果が分かっていれば、後は2次元累積和を求めれば終わりだからです。
1番目と2番目の解法についてそれぞれ見ていきます。
影の条件を無視した時に最適な移動方法というのは、当然直線状に2点間を移動するのが移動距離が最も短くなり正当です。まずは2点間を直接移動できる条件について考えます。
偏角ソート順に頂点番号を割り振り直します。この時、頂点1→頂点3の移動方法は次のようになります。
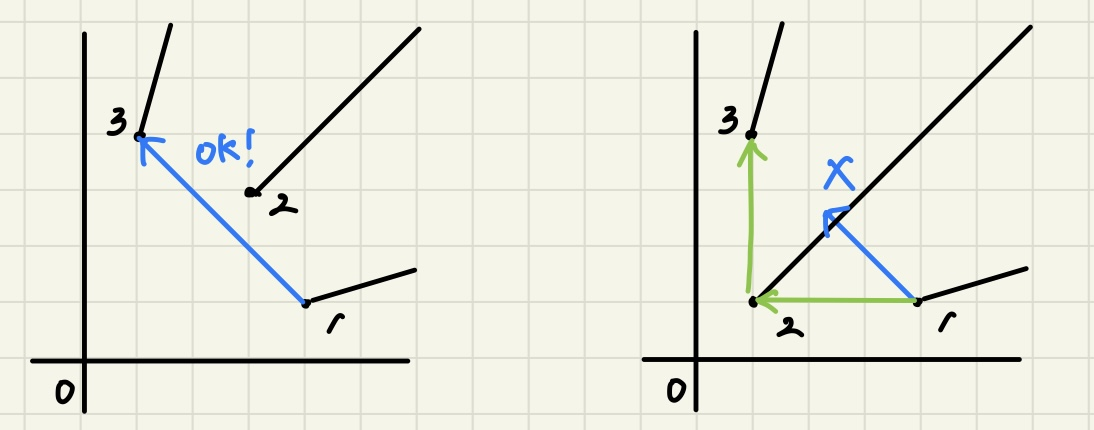
直接移動できない条件は、三角形△O13の内部に他の頂点が存在しないことであり、もし存在した場合の最短経路は右のようになることも分かります。頂点が増えた場合も結局この3頂点の場合に帰着させることが出来て、直線同士の中継点はポールに限る移動のみを考えればよいです。
これで考察はほぼ終わりで、凸包を構築しながらこの移動方法を実装すればOKです。これだけだと分かりにくいと思うので図示したものを掲載します。
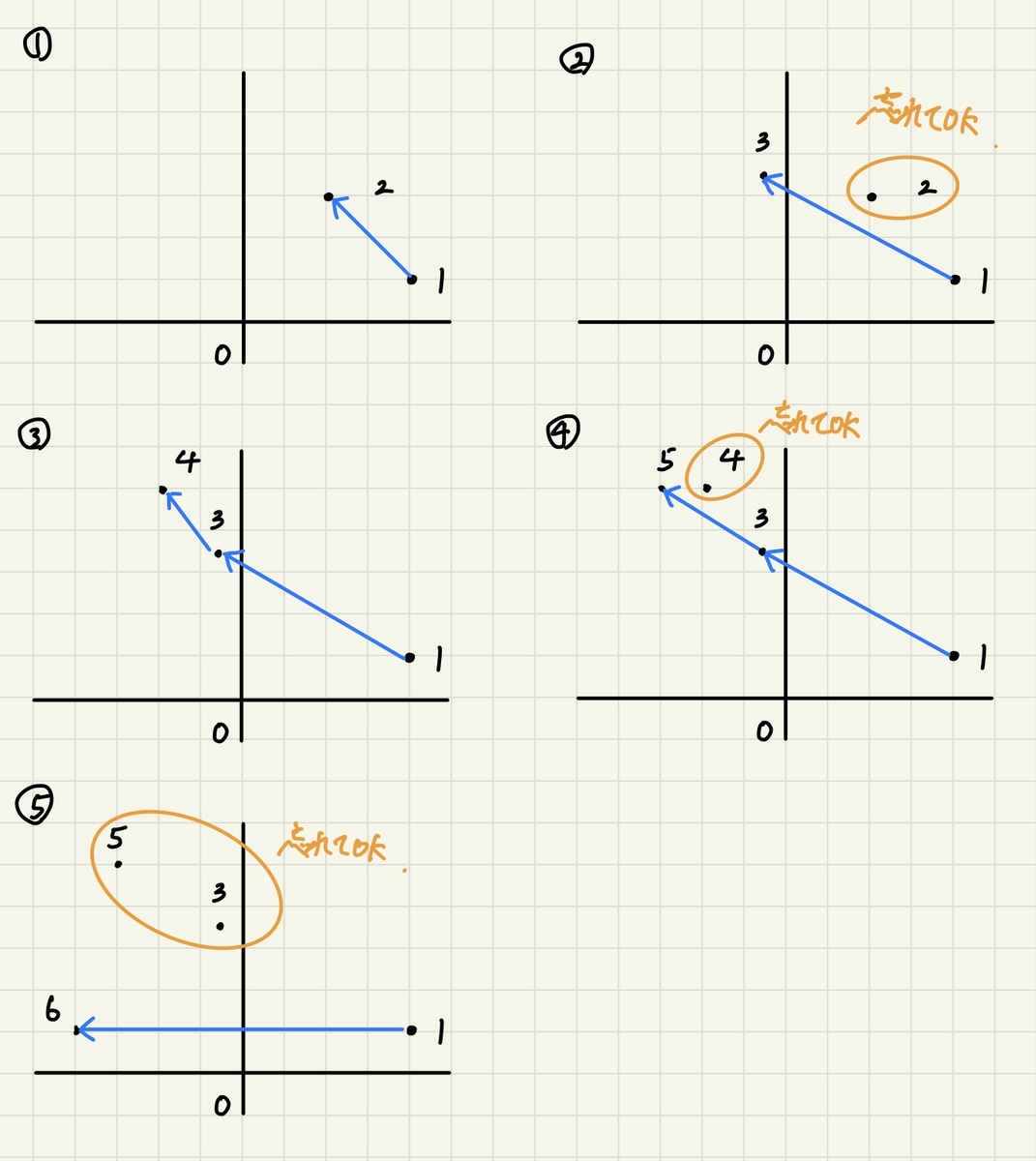
始点を固定するので $ O(N) $、凸法を構築しながら最短距離を計算するので $ O(N) $ で、全体で $ O(N^{2}) $ となっています。
問題の2番目です。$ O(N^{3}) $ の愚直は非常に簡単ですが・・・
vector<vector<double>> res(n,vector<double>(n)); // O(N^3) for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { double mx = 0; for (int k = 0; k < n; ++k) { mx = max(mx, d[i][k]+d[k][j]); } res[i][j] = mx; } }
この問題を解くにあたって、全ての頂点対 について、次の条件を満たす頂点
を求めることにします。
偏角ソート順に見ていった時、
→
→
の順で現れる。
そのような頂点群の中で、上の移動経路が最大となるような頂点。
初期化は、 と定めることにします。これを愚直に求めようとすると、
かかってしまうので、工夫が必要です。
ここで次の事実を用います*1。不等号は偏角ソート順、みたいな感じで受け取ってください(円環なので)。
$$ t _ {i - 1, j} \leq t _ {i, j} \leq t _ {i, j+1} $$
各 について毎回全ての候補を調べていたので、下限と上限が定まっているのは嬉しそうです。また次のように斜めに見ていくと、常に上の不等式が使える事も分かります。
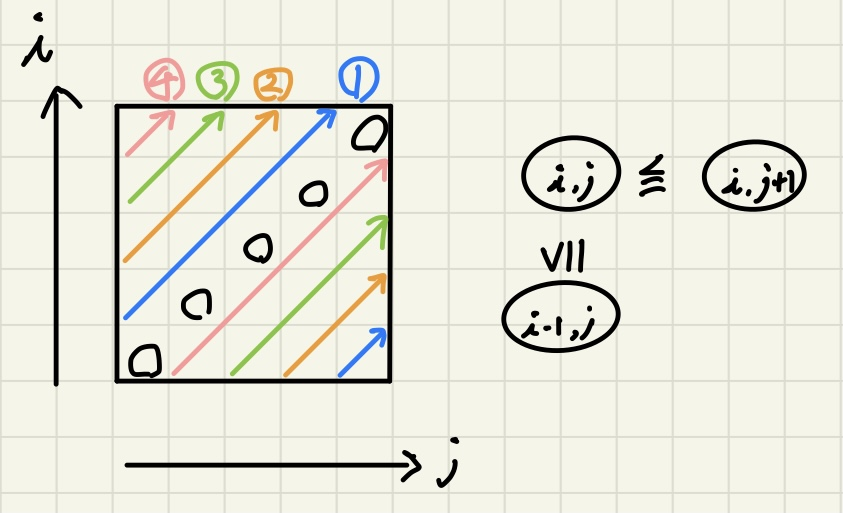
実はこのように探索するだけで、計算量が になっています(!!!)
以下軽い証明です。
$t _ {i,j}$ の候補は、$i$ と $j$ の間にある頂点全てで、これを全てのペアについて足し合わせると、$O(N^{3})$ です。
上の探索範囲で、$t _ {i,j} = x$ と定まったとします。これによって以降どれだけ比較回数を減らせるかについて考えます。$t _ {i+1,j}$ の探索では、$[i + 1, x)$ の範囲を無視できます。同様に、$t _ {i,j-1}$ の探索では、$(x, j-1]$ の範囲を無視できます。
$t _ {i,j}$ の候補の総数から、上記の探索を無視できるペアの総数を引くと、 の項が消えて、全体の計算量は
となっています。
実装
ちなみにですが、AOJのテストケース周りが恐らくバグっていて、c++14ではAC出来ず、c++17のみでACを確認しました*2。
#pragma GCC optimize("Ofast") #include <bits/stdc++.h> using namespace std; typedef long long int ll; typedef unsigned long long int ull; mt19937_64 rng(chrono::steady_clock::now().time_since_epoch().count()); ll myrand(ll B){ return (ull)rng() % B; } struct point{ int x,y; int id; point() {} point(int x,int y) : x(x),y(y) {} point operator- (point p){ return point(x-p.x, y-p.y); } double dist(point p){ return sqrt((x-p.x)*(x-p.x) + (y-p.y)*(y-p.y)); } }; int cross(point a, point b){ return a.x*b.y - a.y*b.x; } int arg_area(point p){ if(p.y < 0) return 2; else if(p.x < 0) return 1; else return 0; } // 整数範囲の偏角ソート 同一点ないと仮定 // 同一偏角の場合は原点に近い方を優先 bool arg_comp(point a, point b){ int ap = arg_area(a), bp = arg_area(b); if(ap != bp) return ap < bp; auto crs = cross(a, b); if(crs == 0) return abs(a.x)+abs(a.y) < abs(b.x)+abs(b.y); else return crs > 0; } int main(){ cin.tie(nullptr); ios::sync_with_stdio(false); int n; cin >> n; vector<point> p(n); for (int i = 0; i < n; ++i) { cin >> p[i].x >> p[i].y; p[i].id = i; } // 偏角ソート sort(p.begin(), p.end(), [&](auto i,auto j){ return arg_comp(i, j); }); vector<vector<double>> d(n,vector<double>(n)); for (int i = 0; i < n; ++i) { int k = i; double sum = 0; vector<int> convex = {i}; for (int j = 1; j < n; ++j) { k++; if(k == n) k = 0; if(cross(p[i], p[k]) < 0) break; while(convex.size() >= 2){ int pre = convex.back(); int s = convex[convex.size()-2]; if(cross(p[k]-p[s], p[pre]-p[s]) <= 0){ convex.pop_back(); sum -= p[pre].dist(p[convex.back()]); } else break; } sum += p[k].dist(p[convex.back()]); convex.push_back(k); d[p[i].id][p[k].id] = d[p[k].id][p[i].id] = sum; } } vector<vector<double>> res(n,vector<double>(n)); vector<vector<int>> t(n,vector<int>(n)); // t[i-1][j] <= t[i][j] <= t[i][j+1] を利用 for (int i = 0; i < n; ++i) { t[i][i] = i; } for (int l = 1; l < n; ++l) { for (int j = 0; j < n; ++j) { int i = (j+l)%n; int k = t[(i-1+n)%n][j]; while(1){ double dis = d[p[i].id][p[k].id] + d[p[k].id][p[j].id]; if(res[p[i].id][p[j].id] < dis){ res[p[i].id][p[j].id] = dis; t[i][j] = k; } if(k == t[i][(j+1)%n]) break; k++; if(k == n) k = 0; } } } for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { res[i][i] = max(res[i][i], d[i][j]+d[j][i]); double mx = max(res[i][j], res[j][i]); res[i][j] = res[j][i] = mx; } } vector<vector<double>> sum(n+1,vector<double>(n+1)); for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { sum[i+1][j+1] = res[i][j]; } } for (int i = 0; i <= n; ++i) { for (int j = 0; j < n; ++j) { sum[i][j+1] += sum[i][j]; } } for (int i = 0; i < n; ++i) { for (int j = 0; j <= n; ++j) { sum[i+1][j] += sum[i][j]; } } auto query = [&](int a,int b,int c,int d)->double{ int cnt = (b-a+1)*(d-c+1); double s = sum[b][d] - sum[a-1][d] - sum[b][c-1] + sum[a-1][c-1]; return s/(double)cnt; }; int q; cin >> q; while(q--){ int a,b,c,d; cin >> a >> b >> c >> d; printf("%.9f\n", query(a,b,c,d)); } }